1 The Problem
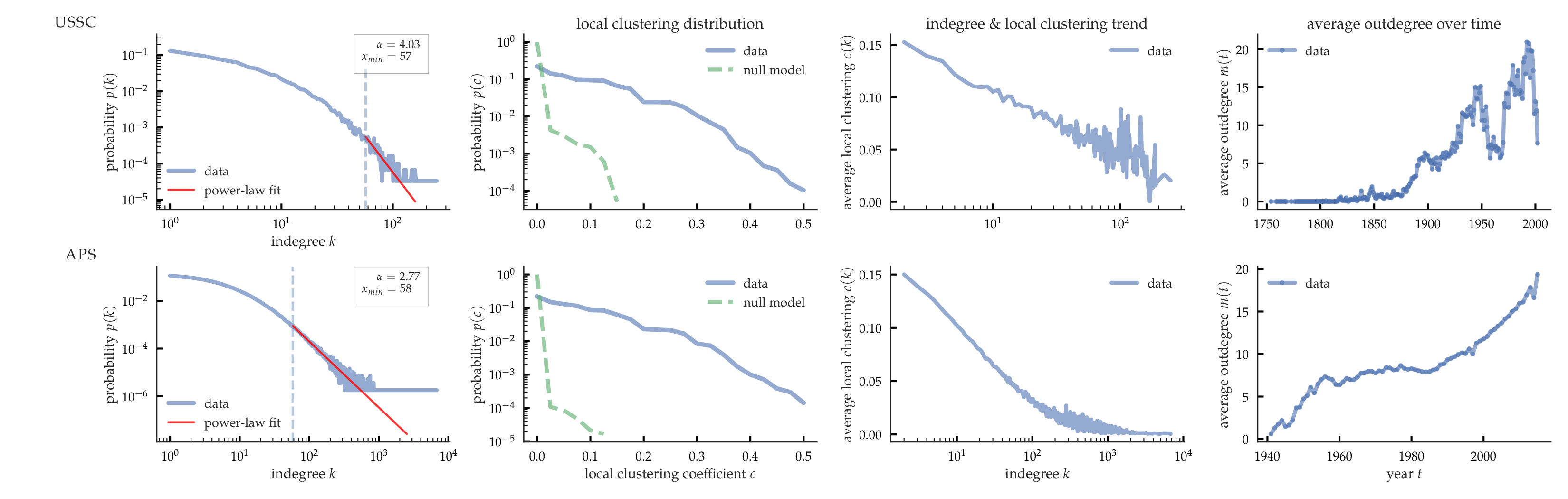
Individuals form connections in social and information networks under constraints of limited information and partial network access. Individuals' edge formation decisions cumulatively shape the structure of large real-world networks. As shown in Figure 1, large-scale academic and judicial networks exhibit rich structural properties: heavy-tailed degree distribution, high clustering and accelerated network growth.
Network growth models study how edge formation mechanisms give rise to distinct macroscopic properties of real-world networks. Classic models of network growth can preserve multiple structural properties, but make unrealistic assumptions about individuals' decisions to form edges. Conversely, existing resource-constrained models do not jointly preserve multiple structural properties of real-world networks.
The problem of developing a model of network growth, where agents act under resource constraints, including access to only local information is hard. The problem lies in identifying simple mechanisms, with few parameters, where the agents only use local information and jointly preserve multiple structural properties of real-world networks.
2 Proposed Model
We propose a resource-constrained growth model in which new nodes that join the network use a random walk process to link to existing nodes. The mechanism that new nodes use to select an entry point into the network and subsequently form edges intuitively corresponds to how we expect researchers to find references to cite. A researcher first finds one or more relevant paper as “starting points”. Then, under time and information constraints, he or she searches for potential references by navigating through a chain of references. After repeating this process one or more times, the researcher selects to cite a subset of these papers.
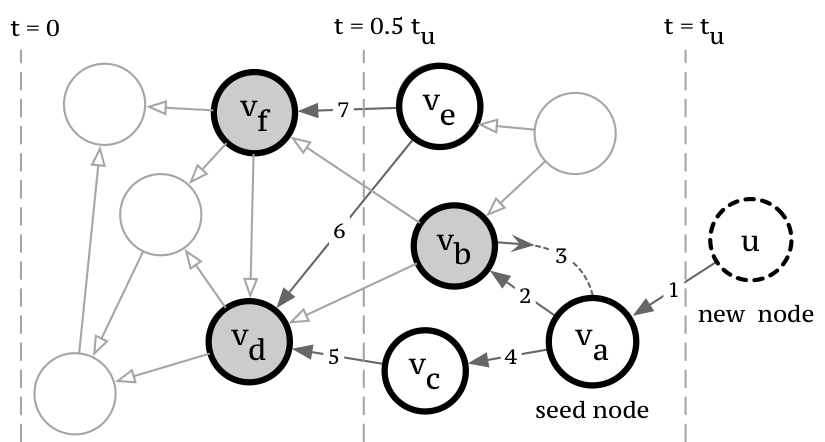
Similarly, as shown in Figure 2, every new node that joins the network selects a seed node from which it initiates the random walk process to search for potential links. The new node terminates the random walk process after linking to a subset of visited nodes. The random walk is parameterized to link to visited nodes, jump back to the seed and traverse outgoing & incoming edges with differing probabilities.
Our model incorporates the resource constraints that influence edge formation as nodes concurrently acquire information and form edges by exploring neighborhoods of existing nodes, without access to the entire network. Moreover, it captures two important sociological phenomena – preferential attachment and triadic closure – as new nodes are more likely to visit & link to popular, high-degree nodes and neighbors of nodes to which it has already linked.
3 Results
We conduct extensive experiments to compare our model against four well-known baseline growth model, which are represetative of common edge formation mechanisms, on five large-scale citation networks. We show that our model can accurately preserve multiple structural properties – heavy-tailed degree distribution, skewed local clustering distribution, degree-clustering relationship – under accelerated network growth.
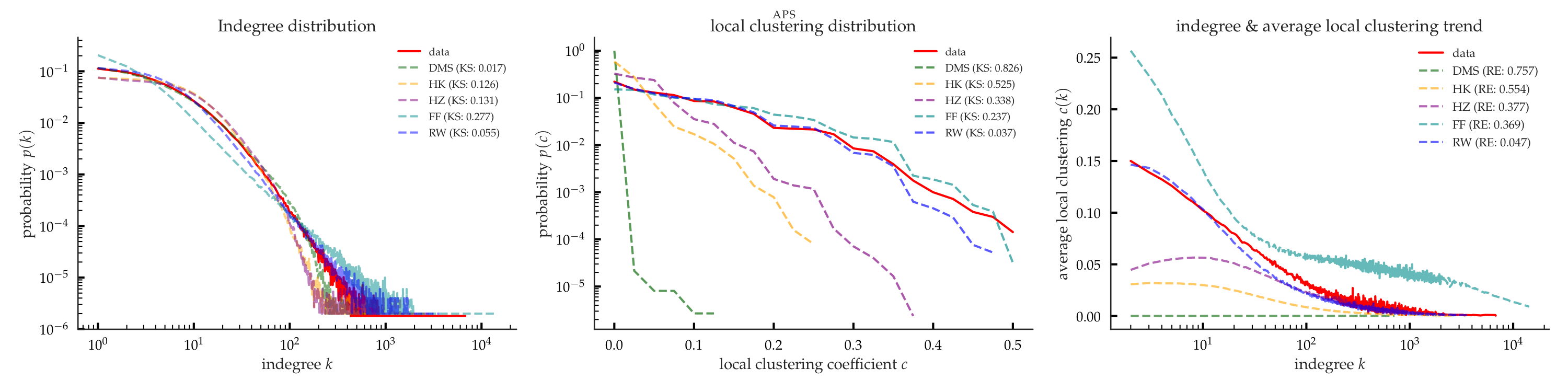
As shown in Figure 3, our model outperforms the baselines in