Online social networks (OSNs) like Twitter, Facebook, and Weibo have become the primary source of publicly available information. These information repositories are of particular interest to several researchers and advertisers interested in understanding social content, including the public opinion, demography, and impact of sociological studies. Researchers may be interested in diverse questions such as: how many different religions have a presence on a social network (attribute discovery)? Identify co-located fans of various sports teams (a clustering problem). Ask if a social network participant is interested in fashion (a classification problem). How does income vary with age and gender (a regression problem)? In this work, we shall see how we can sample content from social networks to answer such content-related queries.
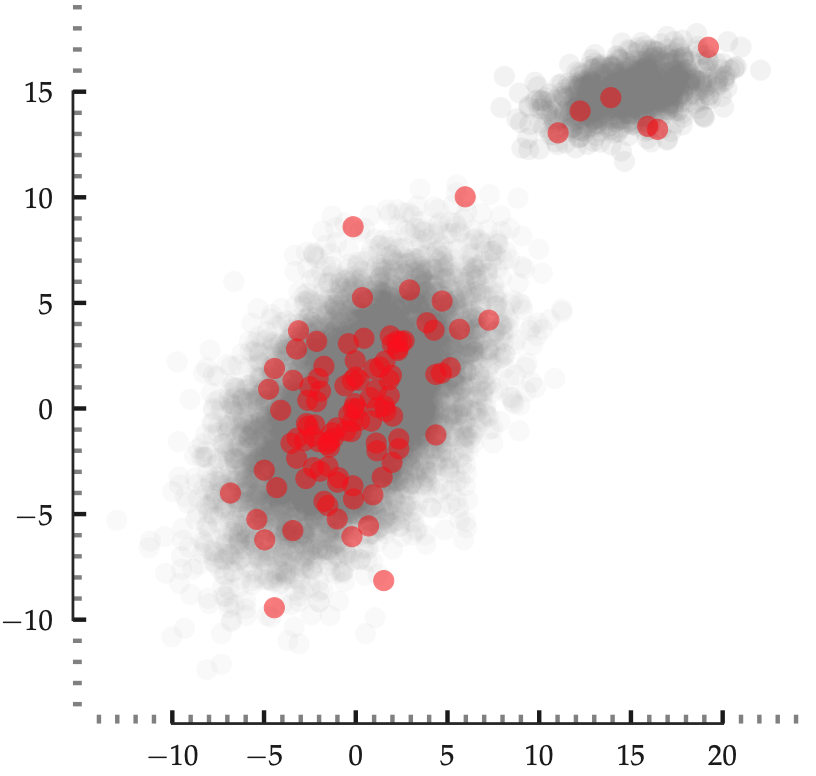
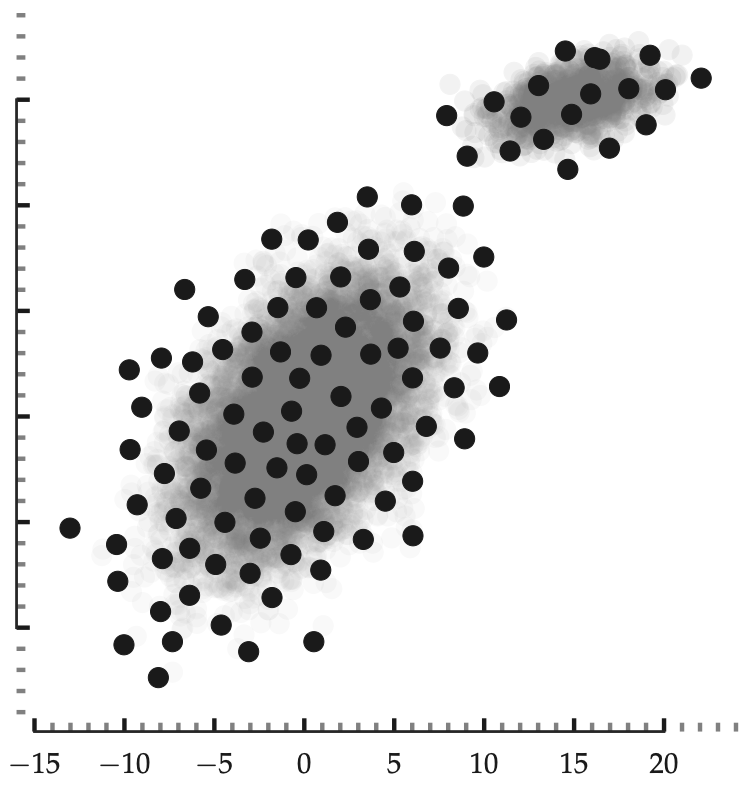
The problem of sampling content from attributed social networks (or graphs) is not trivial. While sampling a graph uniformly at random is essential for characterizing the distribution of attribute values, uniform sampling will pick points around that part of the underlying probability density with the highest concentration of probability mass (see Figure 1). From a clustering or a classification standpoint, the points around the boundary of the class are more informative—sampling the center of the density does not help determine the class boundary. Thus, uniform sampling is not suitable for content sampling because it ignores the arrangement of samples in the underlying feature space, potentially missing out on informative samples useful for tasks like classification or clustering. To address this issue, we propose a task-independent, content sampler (SI) grounded in Information Theory.
Related work
There are several potential strategies to sample content from attributed networks. One popular approach is representative graph sampling that aims to construct a sampled subgraph that has a network structure very similar to that of the original network. Assuming that the content co-varies with the network, we can thus hope to sample representative content by sampling representative network. From various social network analysis 1, we know that this co-variation should occur. However, there are instances where it does not 2. Another line of research focuses on sampling content from an unknown population distribution. Samplers such as Poisson sampling and stratified sampling are shown to be efficient at sampling content from population distribution. However, these samplers require random access to the nodes, which is not typically available in OSNs.
Unlike prior works that have focused on topology and content independently for sampling, we propose a surprise-based sampler that considers both the network topology and content distribution in its design for sampling content.
Proposed Sampling Design
We now describe our proposed surpise-based information sampler (SI) for sampling content from attributed networks.
We show through a toy-example in Figure 2, the workings of SI sampler. SI is a link-trace sampler (or crawler) that uses node attributes (content) to determine the next frontier node (neighbor of sampled node) to add to the current sample set, by checking the content of this node against the content of the nodes in the current sample. In other words, the sampler maintains a knowledge of the OSN’s content by sampling nodes and uses the sampled knowledge to further explore in direction of the most surprising content.
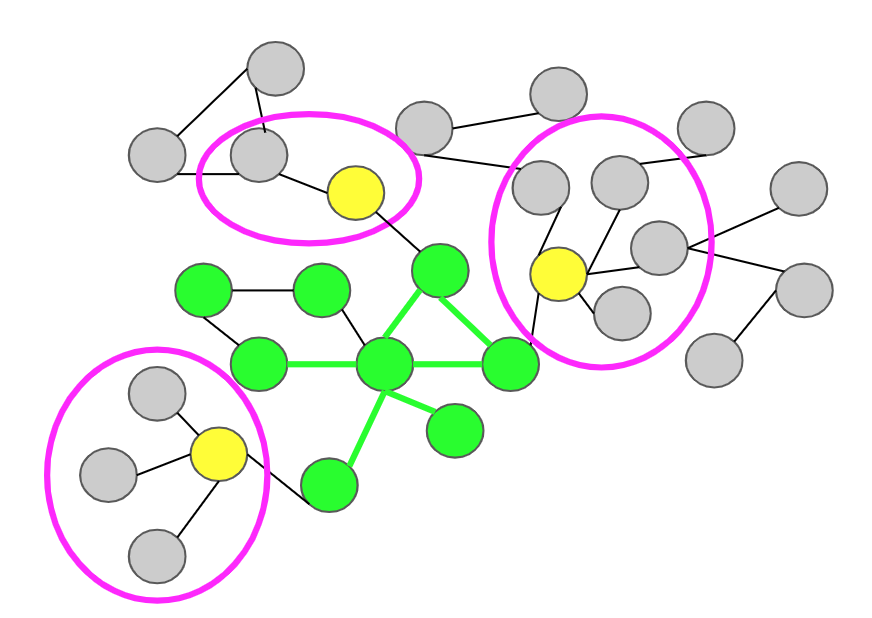
The surprise due to a frontier node $v$ is computed conditional to existing knowledge of the sampler. In the more general case of the SI sampler, $\Delta v \equiv v \cup N(v)$ (neighborhood of $v$) is used to compute the surprise of node $v$. We define the surprise $I_{\Delta v}$ of a candidate set $\Delta v$ (conditioned on sample set $\mathbb{S}$) as follows:
\[I_{\Delta v} =\frac{- \ln P(\Delta v | \mathbb{S})}{|\Delta v|}\]For a set of discrete attribute $\mathbb{A}$, the above surprise definition reduces to,
\[v^\ast = argmax_{v \in N(\mathbb{S})} \sum_{A \in \mathbb{A}} \frac{d(p_{\Delta v}, p_{\mathbb{S}} \mid A)}{|\mathbb{A}|}.\]Thus, we pick the frontier node $v^\ast$ which creates the maximal surprise given the current content distribution in the sampled set $\mathbb{S}$.
For continuous attributes, the surprise due to a frontier node $v$ is defined as,
\[I(\Delta v \mid \mathbb{S}) \propto \frac{|\mathbb{S}| d^2_{\min}}{2} + \frac{\log(2 \pi |\mathbb{S}| |\hat{\Sigma}|)}{2}\]where $d_{\min}$ is the minimum of the distances between the points in $\Delta v$ and the points of the set $\mathbb{S}$, and $\Sigma$ is the sample covariance. Furthermore, we show that the above surprise definition can be approximately reduced to Hausdorff distance for continuous attributes, thereby making SI sampler very efficient to implement in practice.
When the content comprises both continuous and discrete attributes, we employ pareto-optimality to choose the most surprising frontier node.
How does SI sampler perform on real-world tasks?
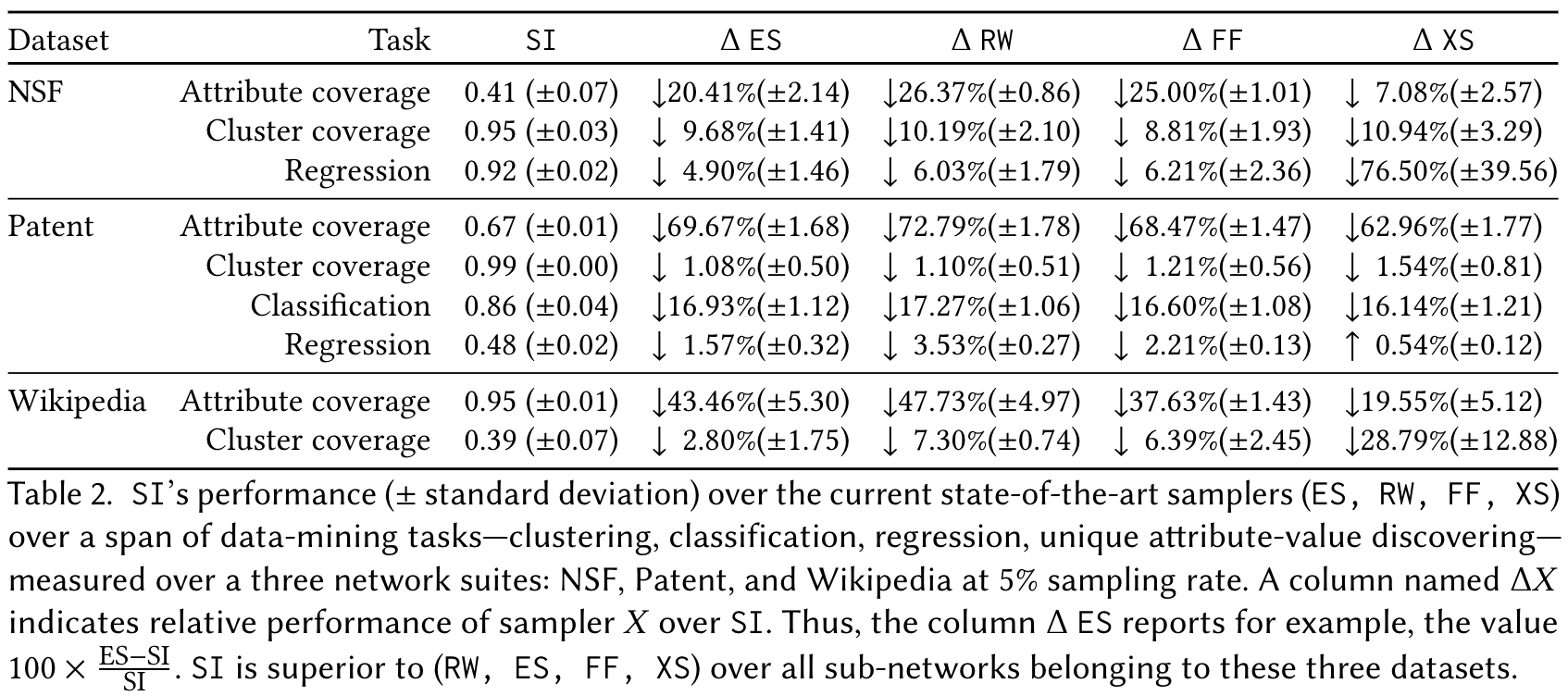
We test our algorithm against standard state-of-the-art graph samplers on several data-mining tasks: attribute coverage, cluster coverage, classification and regression on few representative datasets. SI due to its preference to the surprising content is able to efficiently sample the content structure from online social networks.
Future directions
While several previous studies are limited to specific modes of sampling, e.g., link-trace sampling using the graph APIs, or sampling using attributed search, or sampling using keyword-based search, it will be beneficial to develop samplers that can make use of the multiple query modes simultaneously. Further, real-world datasets often have missing and noisy attributes (content). A robust content sampler that can incorporate such uncertainties and noise in its design will help a number of applications. Finally, we observe that the state-of-the-art samplers are well-suited for network structure preservation, but they fail at preserving the node content. Conversely, SI is suited for preserving the node content but not network structure. A further research goal could be to preserve not just the content but also the latent structural properties (embedding).
Further Information
This blog is based on the paper,
@inproceedings{kumar2020attributeguided,
title = {Attribute-guided network sampling mechanisms},
author = {Kumar, Suhansanu and and Sundaram, Hari},
booktitle = {ACM Transactions on Knowledge Discovery from Data},
year = {2020}
}
