Real-world social and information networks such as Facebook and Semantic Scholar evolve over time as individuals join the network and form connections. Individuals form connections under constraints of limited information (they don’t know who is on the network) and partial network access (typically, one forms connections with people who know you). In addition to resource constraints, well-known sociological phenomena such as triadic closure (an individual will befriend a person with whom they share mutual friends), preferential attachment (a popular person attracts more friends), and attribute homophily (the tendency of like-minded individuals to become friends) also influence individuals’ decisions to form links. Over time, these individual decisions taken together shape the global structure of real-world networks: heavy-tailed in-degree distribution, skewed local clustering, and homophilic attribute mixing patterns.
Can we explain how the different networks that we are part of, emerge?
Network growth models attempt to do so. Consider a simple stylized example: the process of finding a set of papers to cite when writing an article. In the well-known Barabasi-Albert model of preferential attachment, a node making one or more citations would pick papers from the entire network with probability proportional to their in-degree (i.e., number of citations). This process assumes that individuals possess complete knowledge of the in-degree of every node in the network. An equivalent formulation—vertex copying—induces preferential attachment as follows: for every citation, a node would pick a paper uniformly at random from all papers, and either cite it and/or copy its citations. In this case, vertex copying assumes individuals have complete access to the network and form each edge independently. Although both models explain the emergence of power-law degree distributions, they are unrealistic: preferential attachment and vertex copying require global node-level knowledge and complete network access respectively. Additionally, they assume that each edge is formed independently and do not account for the role of attribute homophily (e.g., venue of paper, political interests of Facebook users) in network formation.
More generally, existing network growth models often make one or more of the following assumptions that are at variance with how individuals form edges in attributed networks.
- Complete Information: Individuals have access to the entire network and utilize unbounded computation and information (e.g. node degree) to form links.
- Ignore Nodal Attributes: Individuals solely rely on structural features to form links and do not consider nodal attributes.
- Independence: Individuals form each edge independently of other edges.
We lack an understanding of how edge formation under individual resource constraints shape global network structure of real-world attributed networks. In our recent paper at the Web conference, we first identify commonalities in global network structure and analyze proximity-biased edge formation in attributed real-world networks, which subsequently motivates a local and resource-constrained model of network growth.
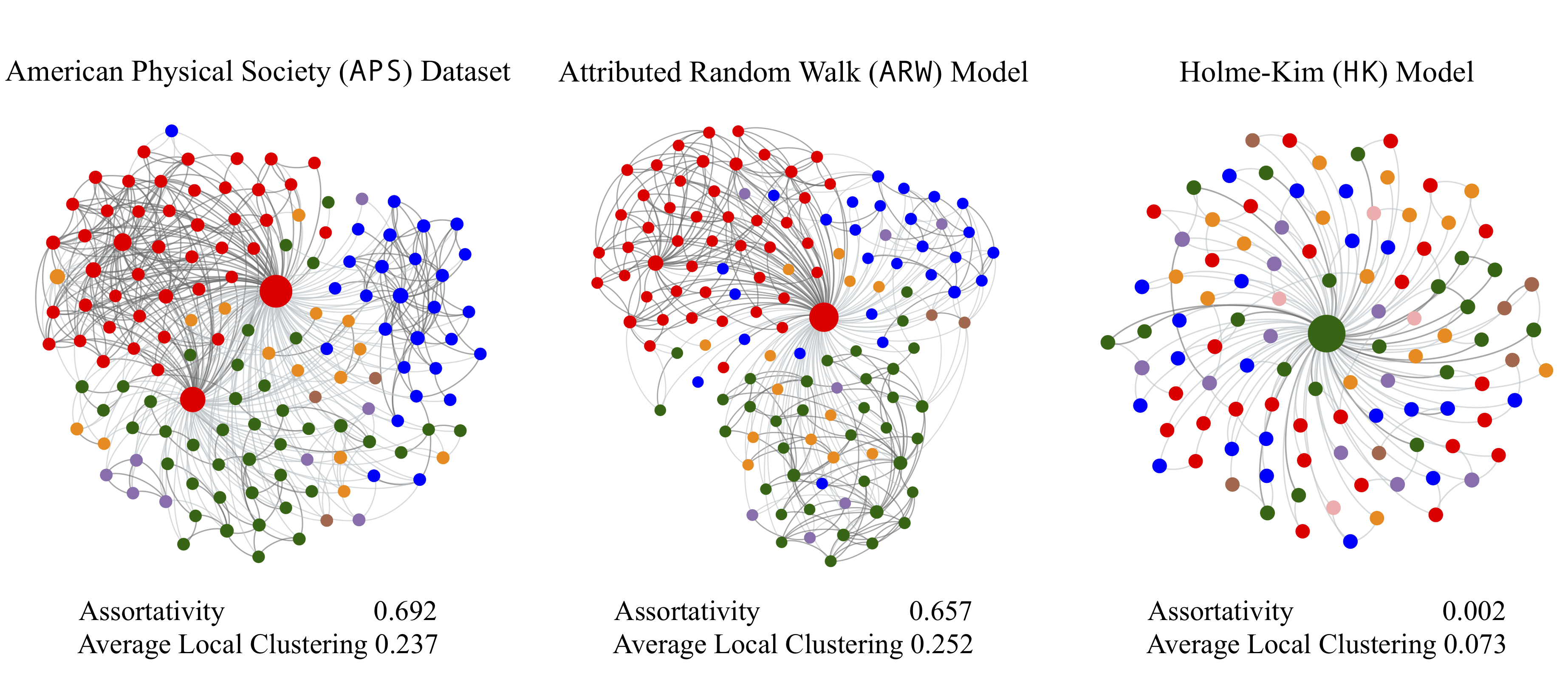
We propose an Attributed Random Walk (ARW) model that unifies multiple sociological phenomena into a resource-constrained edge formation process based on biased random walks to explain how key structural properties of attributed networks emerge over time. Moreover, it accurately preserves key structural properties of real-world attributed networks—in-degree, local & global clustering, attribute assortativity—through an entirely resource-constrained edge formation process.
At a high level, our model is motivated by how new users in social networks navigate their social circles (e.g., friends of friends) to befriend similar others, or how researchers navigate a chain of forward and backward references in papers to survey and cite relevant academic literature. Similarly, incoming nodes in ARW join the network and initiate short random walks to concurrently acquire local information and form edges without recourse to global network access and information. As shown in figure 2, an incoming node selects a seed node based on attribute similarity and initiates a biased random walk. Then, at each step of the walk, it either jumps back to its seed or chooses an outgoing link or incoming link to visit another node; it links to each visited node with probability governed by attribute similarity and halts the random walk after exhausting its budget to form connections.
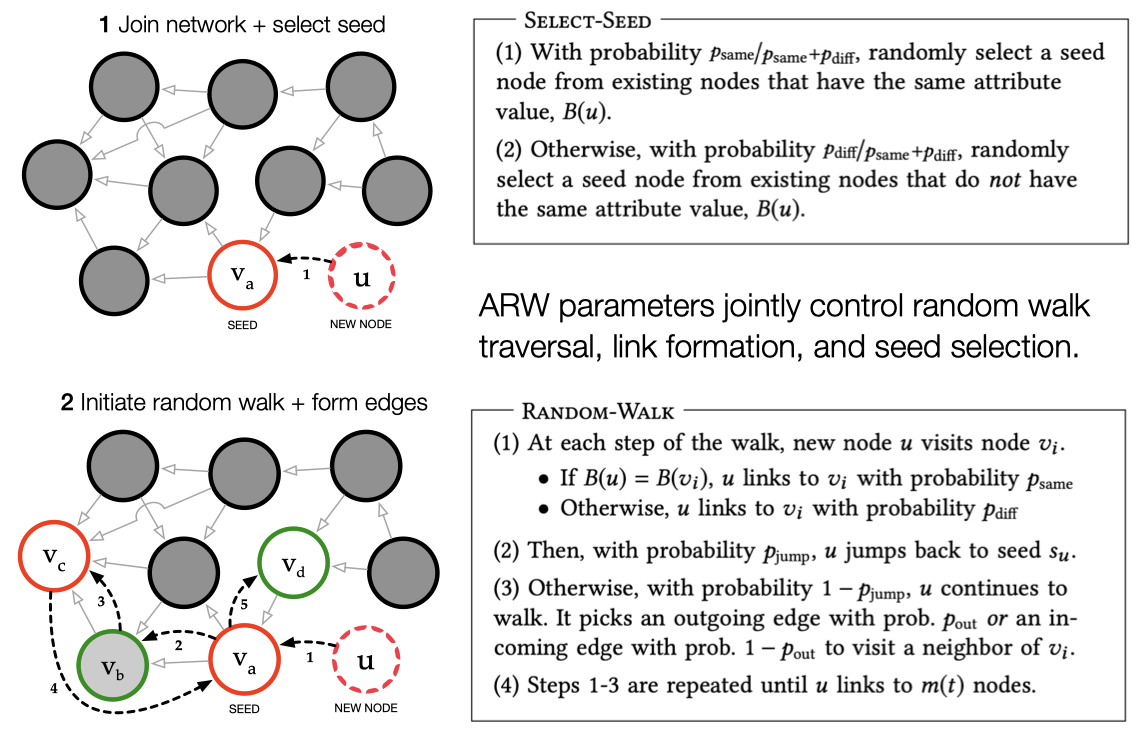
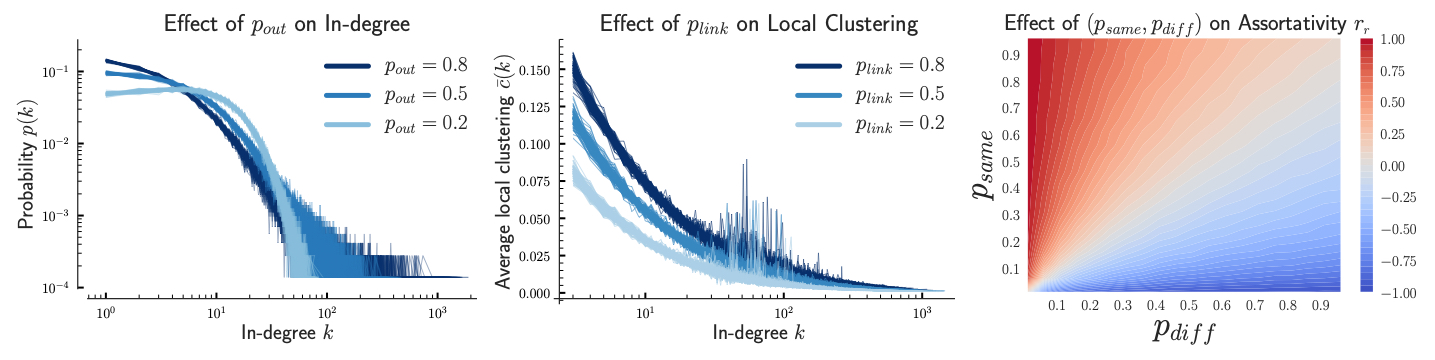
As shown above, ARW consists of four parameters—$p_{\text{same}}, p_{\text{diff}}, p_{\text{jump}}, p_{\text{out}}$— that jointly control seed selection, random walk traversal, and link formation. In particular, attribute-based parameters $p_{\text{same}}$ and $p_{\text{diff}}$ model link formation decisions whereas the jump parameter $p_{\text{jump}}$ and out-link parameter $p_{\text{out}}$ characterize random walk traversals. Furthermore, as shown in figure 3, the model parameters intuitively shape global structural properties—in-degree, local clustering, attribute assortativity— and collectively modulate the extent to which multiple sociological phenomena—triadic closure, resource constraints, preferential attachment, homophily—influence edge formation.
We evaluate ARW’s performance in preserving the global structure of real-world network relative to eight network growth models that are representative of key edge formation mechanisms: preferential attachment, fitness, triangle closing, and random walks. The performance of a model fit is determined by assessing the extent to which the distributional structural properties of the fitted model match that of the observed dataset. Figure 4 below tabulates the performance of ARW relative to eight models in preserving the degree distribution, local clustering distribution, degree-clustering relationship, and attribute assortativity of six network datasets.
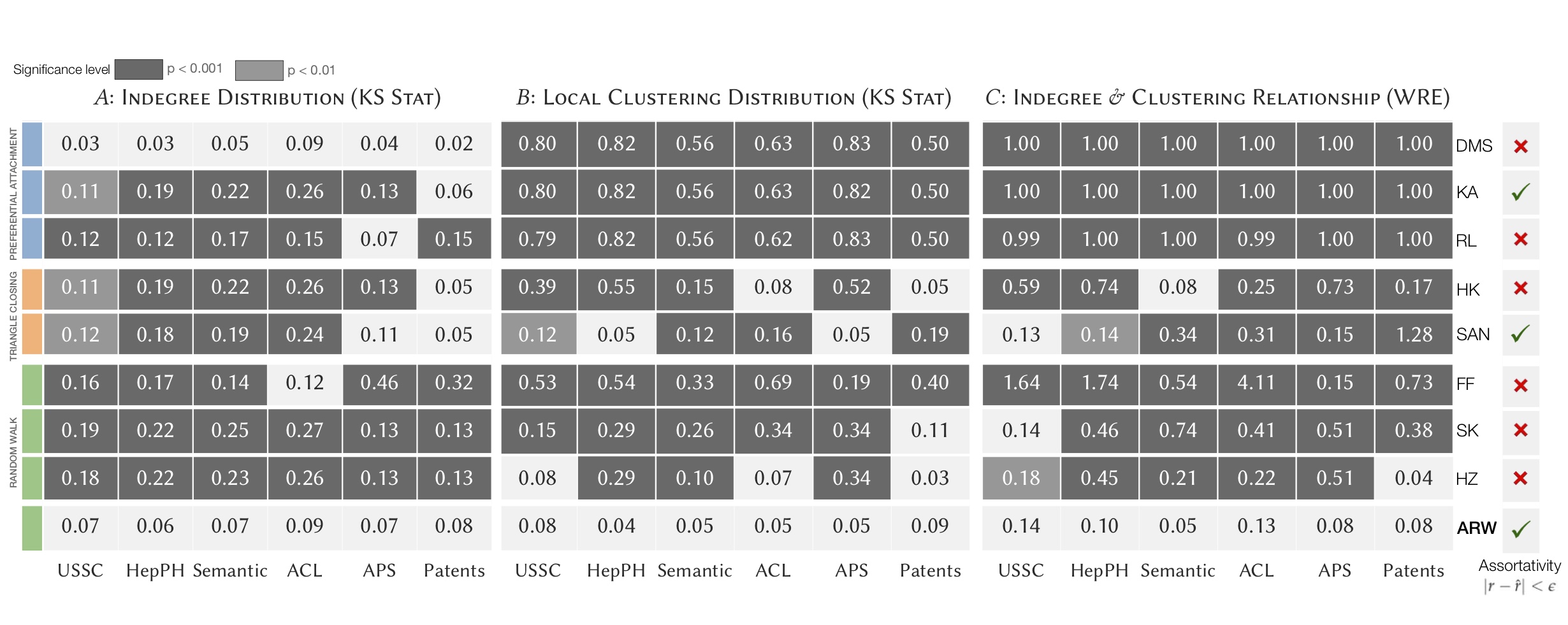
Our experiments indicate that existing models fail to jointly preserve multiple properties because they either disregard triadic closure & attribute homophily or are not flexible enough to generate networks with varying structural properties. Conversely, ARW jointly preserves four key structural properties accurately and generally performs significantly better than existing models by unifying multiple sociological phenomena into a single edge formation process.
tl;dr
Despite the knowledge that individuals use limited resources to form connections to similar others, we lack an understanding of how local and resource-constrained mechanisms explain the emergence of structural properties found in real-world networks. We make three contributions in our paper. First, we propose a simple and accurate model of attributed network growth that jointly explains the emergence of in-degree, local clustering, clustering-degree relationship and attribute mixing patterns. Second, we make use of biased random walks to develop a model that forms edges locally, without recourse to global information. Third, we account for multiple sociological phenomena: bounded rationality; structural constraints; triadic closure; attribute homophily; preferential attachment. Our experiments show that the proposed Attributed Random Walk (ARW) model preserves network structure and attribute mixing patterns of real-world networks significantly better than eight well-known growth models.
You can learn more about our work by reading our poster, paper, and arXiv manuscript. The code is publicly available on Github. Here is the BibTex:
@inproceedings{shah2019growing,
title={Growing Attributed Networks through Local Processes},
author={Shah, Harshay and Kumar, Suhansanu and Sundaram, Hari},
booktitle={The World Wide Web Conference},
pages={3208--3214},
year={2019},
organization={ACM}
}
