Summary
Controlling the largest singular value of linear layers, which is the same as the largest singular value of their Jacobians, not only contributes to the generalization of the model but makes the model more robust to adversarial perturbations. Convolutional layers are a major class of implicitly linear layers that are used in many models in various domains. They are compressed forms of linear transformations with an effective rank that depends on the dimensions of input rather than their filters.
There has been an ongoing effort to design methods for controlling the spectrum of convolutional layers in either trained models or during the training. They are either computationally extensive or rely on heuristics. The algorithms that we present in our work are general and do not assume properties that are specific to dense and convolutional layers The only assumption is that their transformation can be represented as an affine function but the transformation matrix does not necessarily have to be known.
Another main contribution of our work is proving that convolutional layers, unlike linear layers, cannot represent arbitrary spectrums. This limitation has been overlooked by prior works, leading to unexpected behaviors in practice.
What we did
We present an efficient algorithm for extracting the spectrum of any implicitly linear layer, including convolutional layers. This algorithm implements shifted subspace iteration without requiring access to the explicit form of the transformation matrix.

We also provide an efficient method that clips the spectral norm of any implicitly linear layers to arbitrary values, without requiring the knowledge of the explicit form of the transformation matrix.

Combining the two algorithms, we provide an efficient method to control the spectral norm of implicitly linear layers during training. In this method, we do a warm-up on computing the spectral norm and then use the computed singular vectors in the clipping algorithm every 100 steps. This leads to a fast and effective method for controlling the spectral norm, without noticable computational overhead.

Theoretical insights
Here are a summary of our theoretical results:
- We show that PowerQR method is equivalent so shifted subspace iteration algorithm.
- We show how our clipping method performs an exact clipping on linear layers.
- We prove that convolutional layers with circular padding cannot represent arbitrary spectrums. This limitation has been overlooked by prior works and leads to unexpected behaviors in practice for the methods in those works.
Results
- Correctness: Our proposed method is capable of eact clipping for convolutional layers with various types of padding and strides.
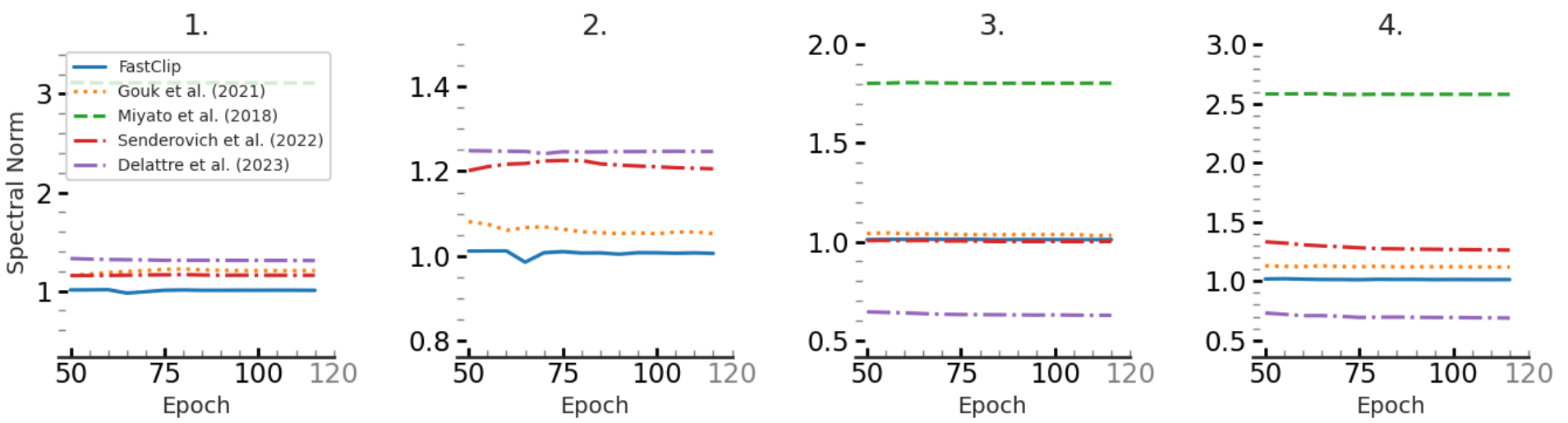
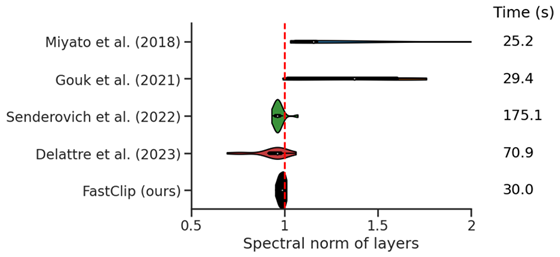
We also show that for clipped ResNet-18 models trained on CIFAR-10, our method more accurately clips the spectral norm of all the layers compared to prior works. The following figure shows the violin plots for the final spectral norm for all the layers when the target value is set to 1.
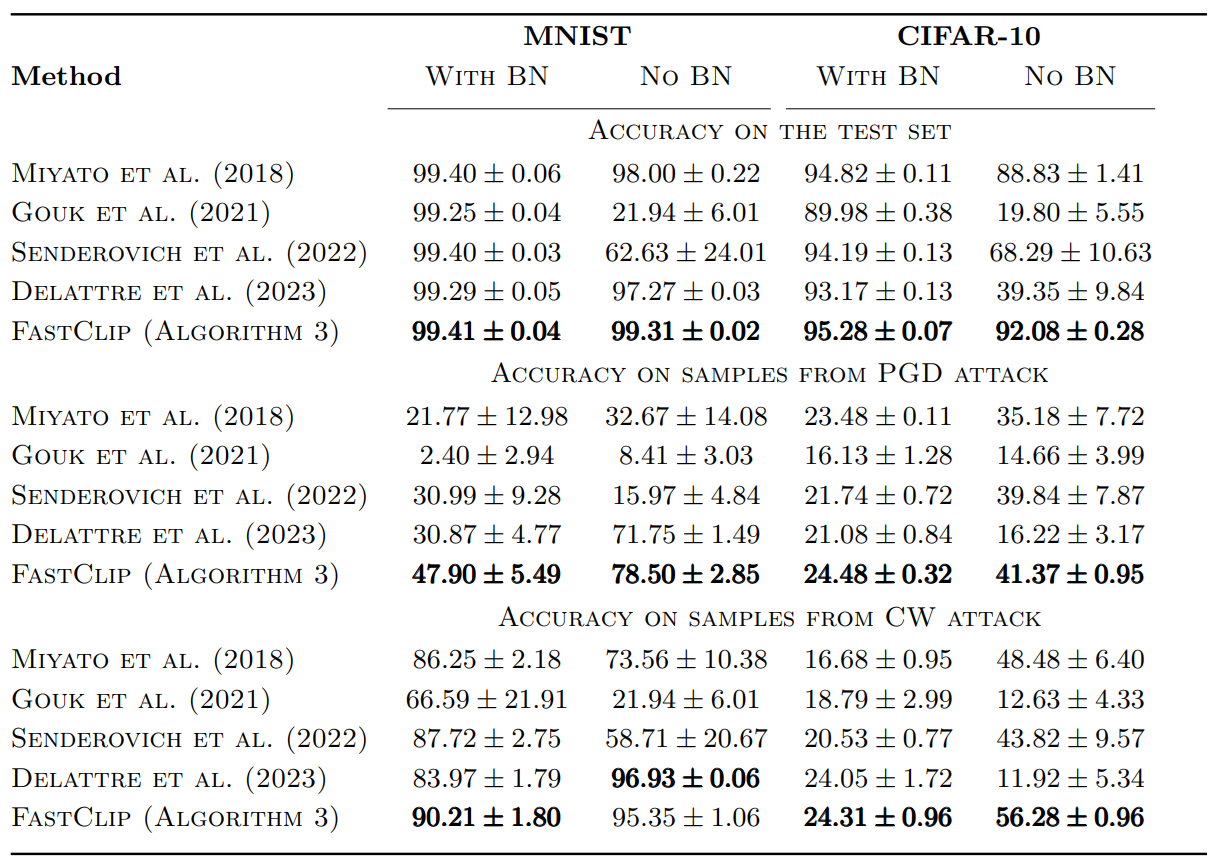
- Robustness and generalization: Our results on ResNet-18 models shows improved test accuracy and robust accuracy against various adversarial attacks.
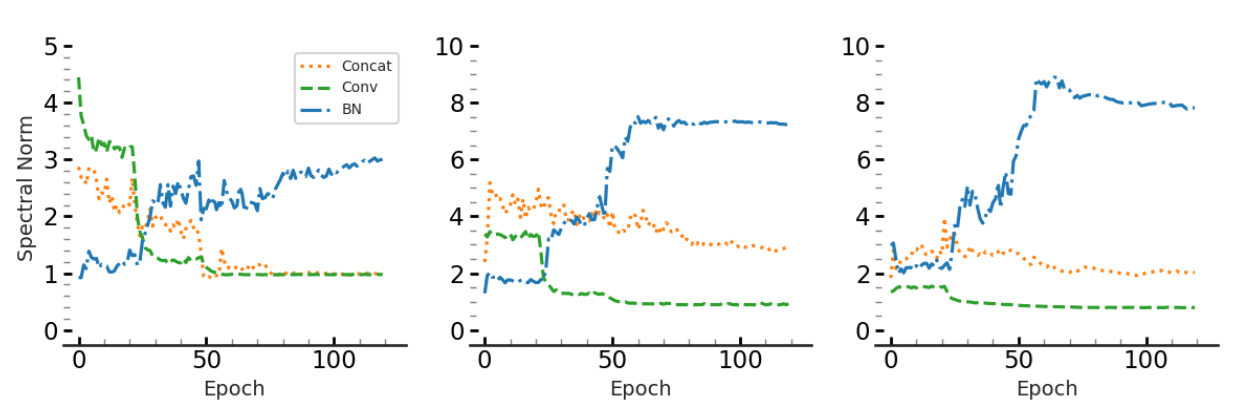
- Effect of batch normalization: As shown in the following plot for the spectral norm of a clipped convolutional layer from a ResNet-18 model, the spectral norm of the composition of convolutional layer and its following batch norm layer becomes large as the training proceeds, despite clipping the convolutional layer. Therefore, to see the effectiveness of clipping in a model that contains batch norm layers, the spectral norm of the compositioan of convolutional layers and batch norm layers have to be controlled as well. Most prior work either ignore this fact or remove the batch norm layers. However, this leads to degradation in model’s accuracy.
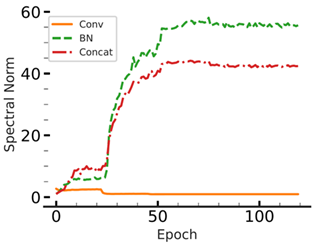
Another interesting phenomenon that we observed is that by clipping the spectral norm of convolutional layers to smaller values, batch norm layers compensate by increasing their spectral norm during training.
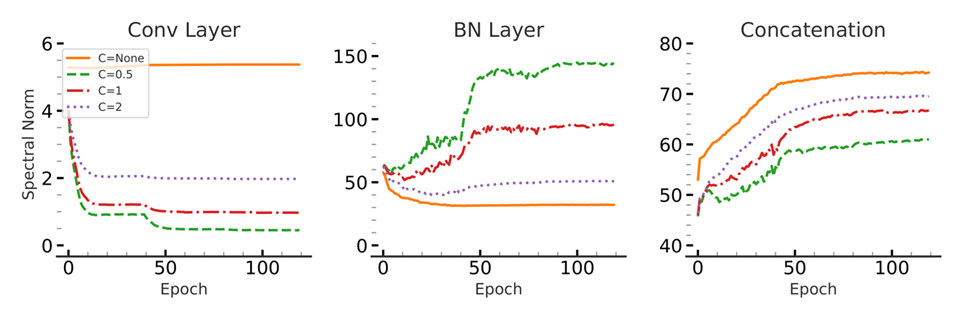
We show that our algorithm can also be used to control (to some extent) the Lipschitz constant of the composition of convolutional layer and their composition with their following batch norm layer.