In a nutshell
Survey responses that reflect respondents’ true preferences are critical. With true preferences, decision-makers at corporations, policymakers, and academics who regularly use surveys would make better-informed conclusions. Our survey tool, Quadratically Constrained Surveys, can help with this challenge for online surveys.
An individual may have nuanced preferences over related options and well-known scales like the Likert scale may prove limiting. Let’s use an example to illustrate our ideas.
Say you are the owner of an ice-cream shop and you’ve introduced five new flavors. Now, you decide to survey customers and use a Likert scale that has three options: “no,” “neutral,” and “yes.” Customers indicate preferences with this scale, for each of the five flavors. Perhaps a customer might indicate “yes” to three of the five flavors, and either “neutral” or “no” to the other two. But the next time they visit, of the three flavors that they liked, they spend \$10 on one flavor, \$4 on the second, and none at all on the third. What you want to know is not what they say in a survey, or which free sample they would choose, but if they would spend their own money on any of these flavors.
Surveys that use the Likert scale or ask for preference ranking struggle with this nuance. In a typical Likert-scale survey, the responses to all the questions are independent, in the sense that respondents are free to indicate anything that they wish for each question. Likert is appropriate when the questions are independent. But when options are not independent as in our ice-cream survey example, where respondents have preferences across options, Likert can prove inadequate. Unfortunately, we can’t address the challenge of accurately estimating preference trade-offs by increasing the granularity of the Likert scale. An alternative to Likert is to ask respondents to rank the flavors. But this approach has its challenges—we cannot know their strength of preference for each flavor.
We need a survey tool that encourages respondents with these nuanced trade-offs, and that helps us to accurately estimate the preference strength and order among preferences.
Lalley and Weyl’s idea of Quadratic Voting, motivated the design of our quadratically constrained surveys. Their work aims to improve voting outcomes in elections. Essentially, instead of voting once for a candidate, voters can vote multiple times for a candidate, but the cost of each vote increases quadratically. All citizens receive a finite number of voice credits to pay for votes. The more a voter spends on a candidate, the more they value that candidate. The quadratic nature of vote costs is critical—it prevents someone from quickly buying up a large vote share. Intrigued by this idea, we wondered if we could apply a similar idea to online surveys, to address the challenge of eliciting preferences across related options.
We developed a novel interface for online surveys—Quadratically Constrained Surveying (QS). In QS, respondents can indicate the strength of their preference for each option, but with a quadratic cost. To continue our example, if a respondent wants to indicate a strong preference for option A, they may wish to up-vote that option four times, but this will cost them 16 credits. Similar upvoting twice for option B will cost 4 credits, and upvoting once for option C will cost 1 credit. Notice that downvoting an option (say option D) twice will also cost 4 credits. The catch in QS is that we endow respondents with a small number of credits (i.e., a budget), and respondents can only spend up to their credit budget across the different options. Importantly, due to the budget, they cannot give all of the options a high score, as they might with Likert.
In sum, QS elicits preference strengths like Likert (but with more nuance) and preference order like preference ranking. Dynamically updating the quadratic costs for votes and computing the credits remaining are best accomplished with an online interface. Our main finding is that QS causes survey respondents to more accurately reveal their preference strength and preference ranking than traditional scales.
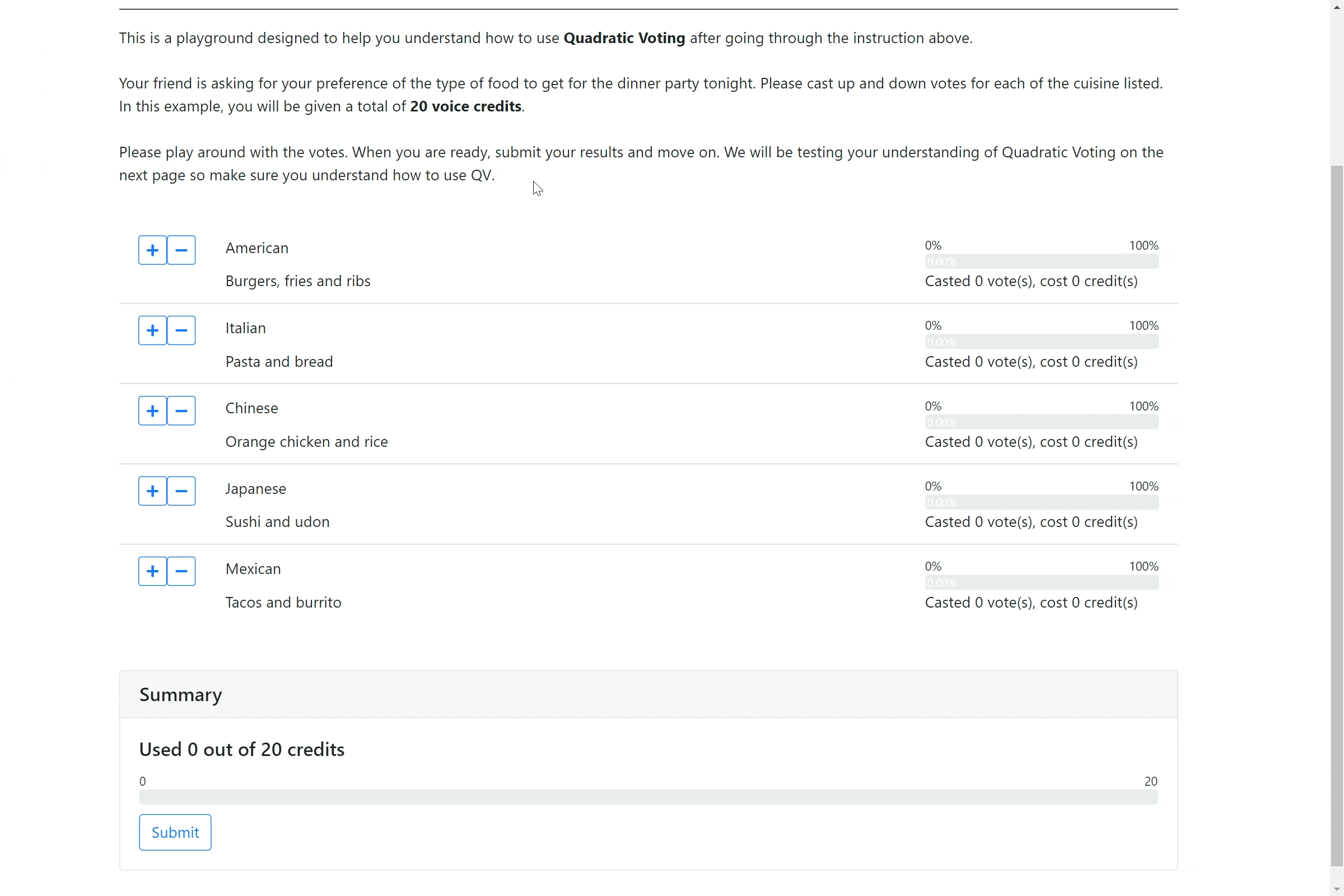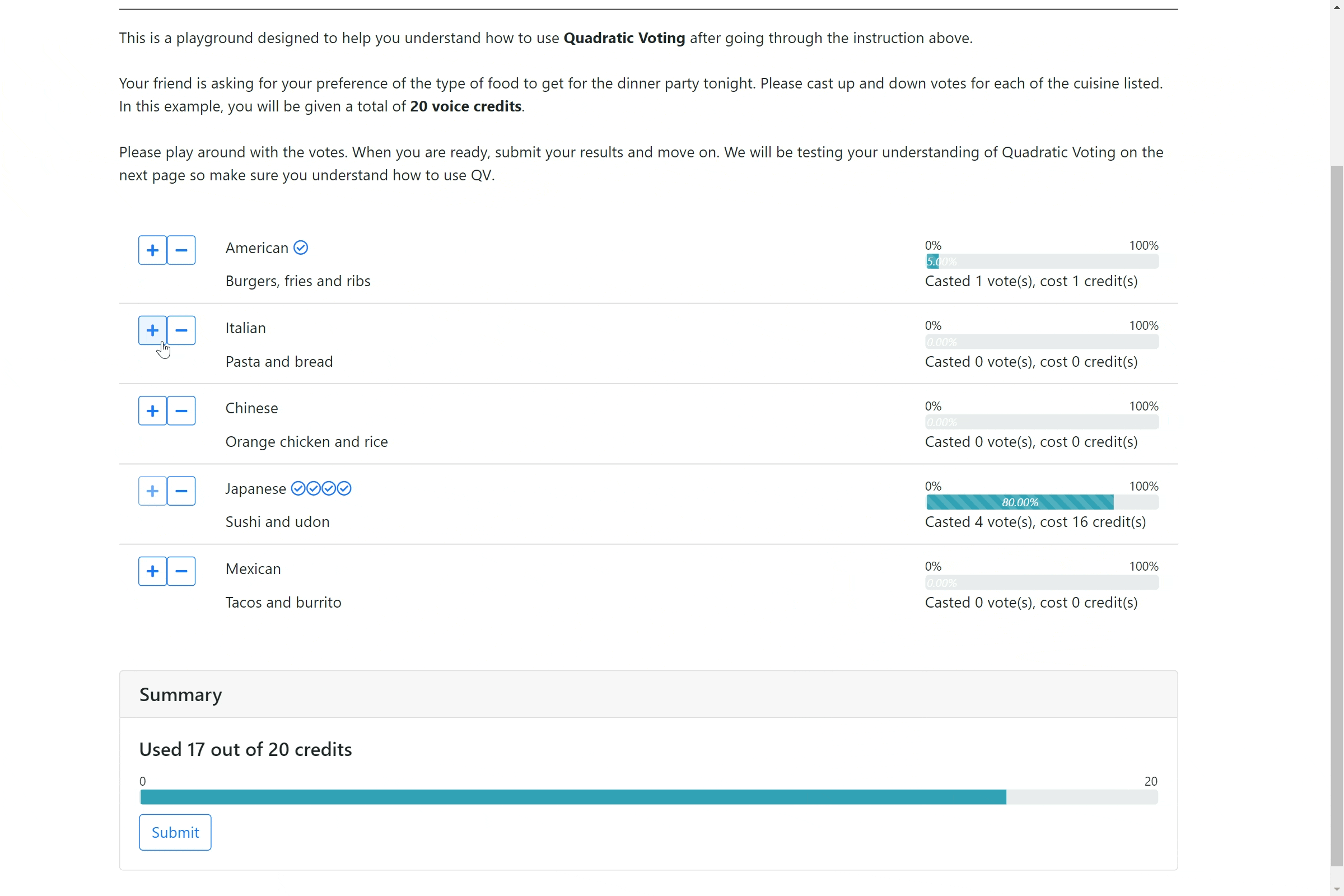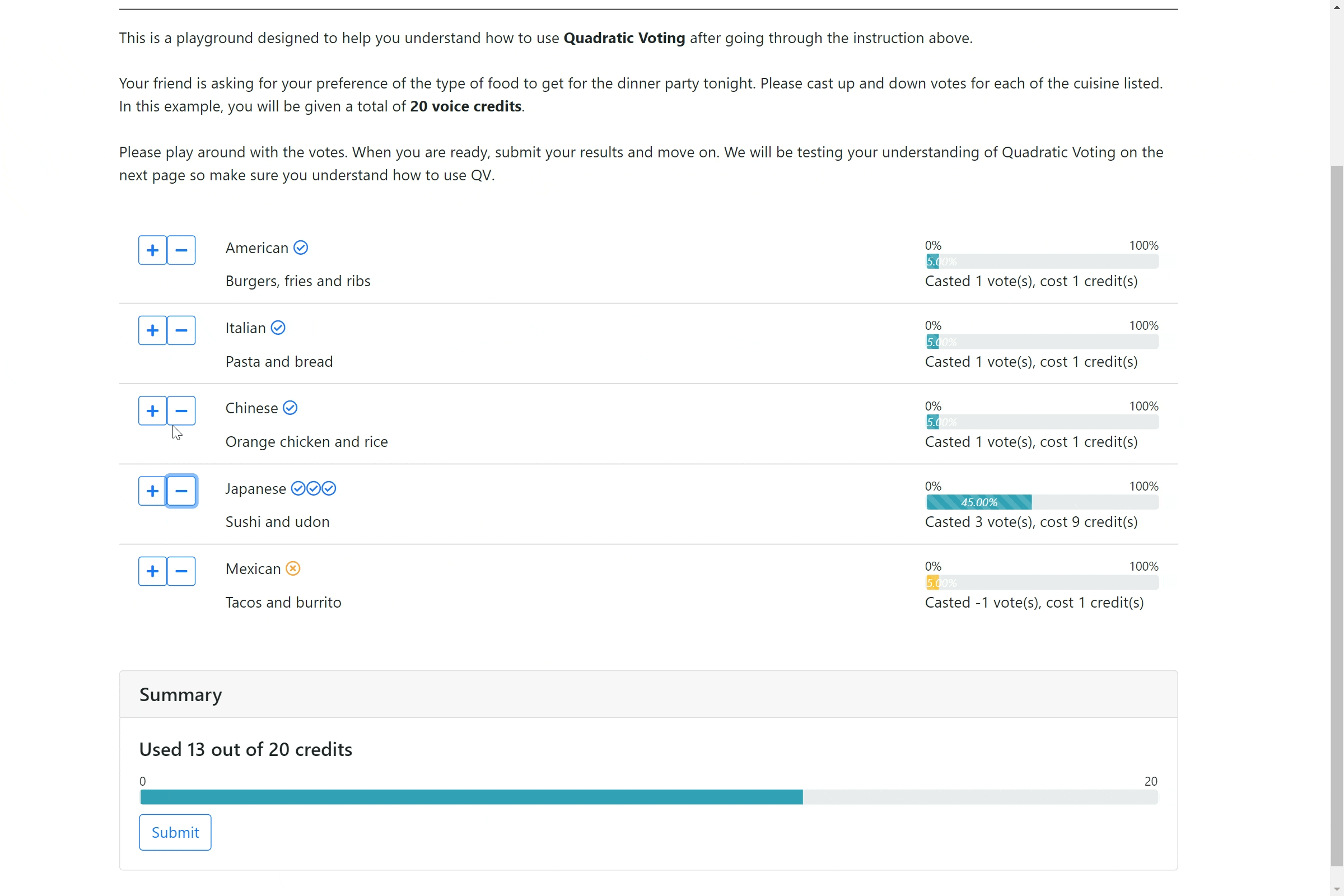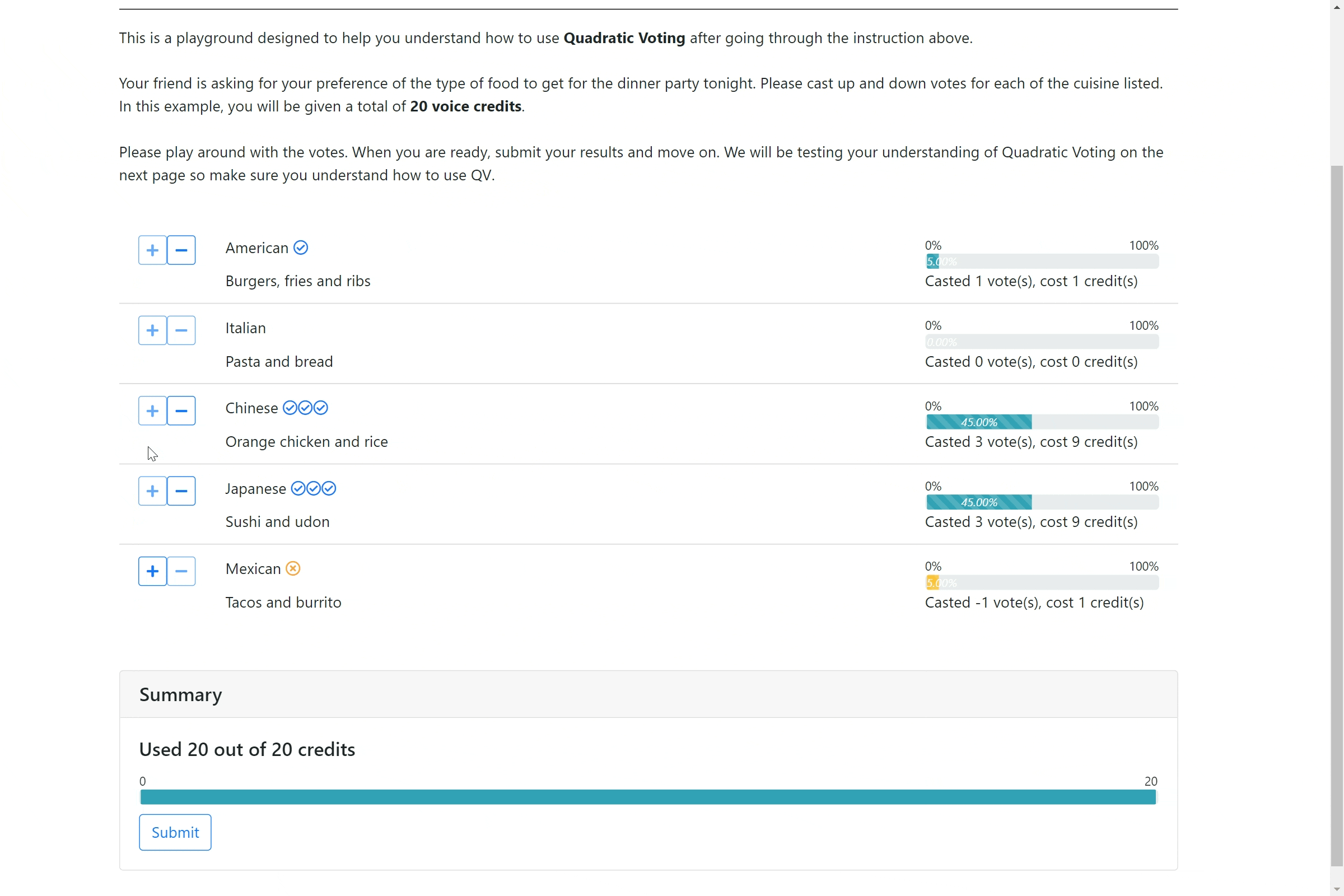
The effect of the budget (i.e., the total number of credits available to pay for votes) in QS is subtle, but key. The budget induces a scarcity mindset in the respondent making them “trade-off” between the options. Shah, Shafir, and Mullainathan conducted an intriguing study examining when individuals behave rationally. They found that inducing scarcity during decision-making, makes the trade-off heuristic more accessible, and results in individual behavior closer to the rational ideal..
Both the quadratic costs of options and a finite budget are necessary for QS to work. We find that either making costs linear (and having a budget), or removing budget constraints (but keeping quadratic costs) are both not significantly different from using the Likert scale.
In More Detail
We conducted two experiments on Amazon MTurk platform to compare Quadratically constrained surveys (QS) to Likert-scale surveys. The first experiment involved a decision with $K$ choices independent of each other (towards which societal cause should the government spend?). The second experiment examined a decision with $K$ options jointly contributing to the outcome (video viewing experience). We randomly assigned each participant to either the QS or the Likert condition in each experiment.
To understand if the preferences in either QS or Likert reflected the participant true preferences, we added one more step to the experiment. We entered each participant into a lottery, where they had a chance of winning \$35. Then, we asked each participant, if they won \$35, how much of their winnings they would donate to each of the $K$ options (charities in the first experiment, aspects of the video-watching preference in the second experiment). Notice that a rational subject would never donate their winnings; thus, any donation towards an option reflects the strength of their true preference towards that option.
We then compared the preferences elicited via QS and Likert to those elicited via the donations towards the choices in the second step. We find that the preferences elicited from the QS survey aligned significantly better with the true-preferences behaviors than the Likert-scale survey. The number of credits to spend across options (i.e., the budget) matters too: medium and large budgets yielded better alignment than small budgets.
What is key: the scarcity mindset or the quadratic costs? Might the results have been different if the costs for each vote were linear instead of quadratic? After all, if making trade-off thinking more accessible was key, then linear costs should work too. And what if there was no budget constraint? We conducted a third experiment to test these questions. Our preliminary results suggest that a linear cost (but with a finite budget) to vote was not significantly different from Likert in the effectiveness of eliciting preferences. And, we found that removing the budget constraint while keeping quadrtic costs for votes, was also not different from Likert. These results suggest that the scarcity mindset is not the only reason why QV works. A finite budget (to induce scarcity) and quadratic vote costs are both necessary.
What’s next?
Our study is a starting point for understanding and deploying Quadratically constrained Surveys. Our work led us to many interesting questions. QS requires understanding an novel interface for responding to a survey, whereas Likert-scale is easy to understand. To make QS broadly accessible, we need to understand how individuals reason about choices in this new interface, and with this understanding, design more accessible interfaces.
You can find more details about our research in our paper.. We are working on a QV platform, http://surveyish.org to make QV-based surveys widely accessible to all scholars.
Resources
@article{10.1145/3449281,
author = {Cheng, Ti-Chung and Li, Tiffany Wenting and Chou, Yi-Hung and Karahalios, Karrie and Sundaram, Hari},
title = {"I Can Show What I Really like.": Eliciting Preferences via Quadratic Voting},
year = {2021},
issue_date = {April 2021},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {5},
number = {CSCW1},
url = {https://doi.org/10.1145/3449281},
doi = {10.1145/3449281},
journal = {Proc. ACM Hum.-Comput. Interact.},
month = {apr},
articleno = {182},
numpages = {43},
keywords = {likert scale, quadratic voting, collective decision-making, empirical studies}
}
@data{illinoisdatabankIDB-1928463,
doi = {10.13012/B2IDB-1928463_V1},
url = {https://doi.org/10.13012/B2IDB-1928463_V1},
author = {Cheng, Ti-Chung and Li, Tiffany Wenting and Karahalios, Karrie and Sundaram, Hari},
publisher = {University of Illinois at Urbana-Champaign},
title = {Dataset for '"I can show what I really like.": Eliciting Preferences via Quadratic Voting'},
year = {2021}
}
